一种基于状态空间的启发式搜索算法及其实现
摘 要:深度优先和广度优先搜索算法由于需遍历所有状态空间才能求出最佳解,使其在状态空间较大时效率极低,此时必需采用启发式算法实现快速求解。阐述启发式搜索算法在状态空间较大时的广泛应用,深入分析一种启发式算法-AStar算法实现快速求解的原理,并详细介绍了其实现步骤及过程。最后,得出结论:基于合理估价函数的AStar算法能极大提高求解效率。
关键词:启发式算法;AStar算法;状态空间;估价函数
中图分类号:TP393 文献标识码:B 文章编号:1004373X(2008)1607902
Heuristic Search Algorithm and Its Implementation Based On State Space
ZHANG Sheng
(Communication and Command Academy,Wuhan,430010,China)
Abstract:Depthfirst and breadthfirst searching algorithm must traversal all state space to seek out the optimum solution,their efficiency is extremely low when the state space is big.In this case,heuristic algorithm can work quickly to get the solution.Heuristic algorithm′s wide application is stated in the large state space.Furthermore,one kind of Heuristic algorithm′s principleA-Star algorithm is analysed thoroughly,the process and the steps of its realization are described in details.Finally,a conclusion is drawn:AStar Algorithm based on reasonable evaluation function can improve the solution efficiency enormously.
Keywords:heuristic algorithm;AStar algorithm;state space;evaluation function
1 引 言
基于状态空间的路径搜索,即将问题求解过程表现为从初始状态到目标状态寻找路径的过程,普通应用于各个领域。基于状态空间的路径搜索算法通常可分为3类:深度优先搜索算法、宽度优先搜索算法(或称广度优先搜索算法)和启发式搜索算法。前两种算法均需在给定的状态空间中穷举,以求解中最佳路径,其非常适合状态空间不大时的求解,但当状态空间十分大,且不预测的情况下,他们的效率极低,甚至不可完成。而启发式搜索算法在状态空间搜索时,对每一个搜索的节点进行评估,得到最佳的节点,再从这个节点进行搜索直到目标节点,可省略大量无谓的搜索路径,极大提到效率,这使得其在状态空间较大的领域得到了广泛应用,如自驾车路线、网络传输路径、游戏中角色行走路线等。
2 启发式算法
在状态空间搜索时,为了更有效地搜索一个给定的状态空间,可设计一个估价函数来决定每一次扩展时,哪一个节点最有希望到达目标节点,然后搜索就可能沿着某个被认为是最有希望的节点向外扩展。如果能够给定一个比较合适的估价函数,将会大大的减少搜索工作量。对节点的估价十分重要,采用不同的估价可以有不同的效果。估价函数可表示为:f(n)=g(n)+h(n) 其中f(n)是节点n的估价函数;g(n)称为“深度因子”,在状态空间中从初始节点到节点n的一条最佳路径的实际代价;h(n)是从节点n到目标节点的一条最佳路径的估计代价。f(n)的值就是从初始节点开始约束通过节点n的一条最佳路径的代价,而最小的f(n)值的节点就是所估计的加有最少严格约束条件的节点。不难发现,搜索的启发信息主要由h(n)来体现,因为g(n)是已知的,其代表了搜索的广度的优先趋势。
3 AStar算法
启发式搜索算法有局部择优搜索法、最好优先搜索法等。其均使用了启发函数,但在具体的选取最佳搜索节点时策略不同。如局部择优搜索法在搜索的过程中选取“最佳节点”后舍弃其他的兄弟节点和父亲节点,而一直搜索下去。由于其舍弃了其他的节点,可能也把最好的节点舍弃,因为求解的最佳节点只是在该阶段的最佳并不一定是全局的最佳。最好优先算法克服了这种不足,在搜索时,并没有舍弃节点(除非该节点是死节点),在每一步的估价中都把当前的节点和以前的节点的估价值比较得到一个“最佳节点”,可以有效地防止“最佳节点”的丢失。
AStar算法是一种加上一些约束条件的最好优先的算法。当状态空间较大时,希望能够求解出状态空间搜索的最短路径,即用最快的方法求解问题,AStar算法正是基于这种思想。
如果一个估价函数可以找出最短的路径,称之为可采纳性。AStar算法是一个可采纳的最好优先算法。AStar算法的估价函数可表示为:f′(n)=g′(n)+h′(n) 其中,f′(n)是估价函数;g′(n)是起点到节点n的最短路径值;h′(n)是节点n到目标的最短路径的启发值。由于f′(n)不可预知,其可近似于上面提到的f(n)。当g(n)≥g′(n)时(通常情况下均满足),g′(n)可由g(n)代替。当h(n)≤h′(n)时,h′(n)可由h(n)代替。可以证明应用这样的估价函数是可以找到最短路径的,也就是可采纳的。
应用此估价函数的最好优先算法即AStar算法,其在每一步的估价时,把比较当前节点和以前节点的估价值,以确定“最佳节点”。
4 A算法实现步骤及过程
如图1所示状态空间A到N,欲用AStar算法求起始节点A到目标节点M的路径,括号内为该节点的估价值。
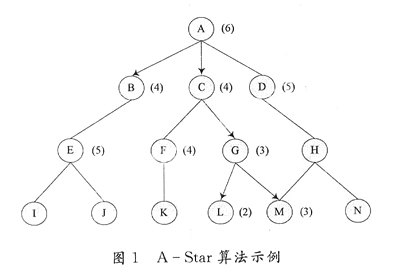
AStar算法示例AStar算法搜索时需设置2个表:OPEN表和CLOSED表。OPEN表保存所有已生成而未考察的节点,CLOSED 表记录已访问过的节点。算法中有一步为根据估价函数重排OPEN表。这使得循环的每一步只需考虑OPEN表中状态最好的节点。具体搜索过程如下:
Step 1:状态初使化
OPEN={A(6)};CLOSED={};
Step 2:估算A(6),取得所有子节点,并放入OPEN表中;
OPEN={B(4),C(4),D(5)};CLOSED={A(6)};
Step 3:估算B(4),取得所有子节点,并放入OPEN表中;
OPEN={C(4),E(5),D(5)];CLOSED={B(4),A(6)};
Step 4:估算C(4);取得所有子节点,并放入OPEN表中;
OPEN={G(3),F(4),E(5),D(5)};CLOSED={C(4),
B(4),A(6)};
Step 5:估算G(3),取得所有子节点,并放入OPEN表中;
OPEN={L(2),M(3),F(4),E(5),D(5)};CLOSED=
{G(3),C(4),B(4),A(6)};
Step 6:估算L(2),取得所有子节点,并放入OPEN表中;
OPEN={M(3),F(4),E(5),D(5)};CLOSED={ L(2),
G(3),C(4),B(4),A(6)};
Step 7:估算M(3),解求完成。
下面是相应的伪程序:
Search()
{ Open = [起始节点]; Closed = [];
while ( Open表非空 ) {
从Open中取得1个节点X,并从OPEN表中删除。
if (X是目标节点) {
求得路径PATH;返回路径PATH;}
for (每一个X的子节点Y){
if( Y不在OPEN表和CLOSE表中 ){
求Y的估价值;并将Y插入OPEN表中;}
else
if( Y在OPEN表中 ) {
if( Y的估价值小于OPEN表的估价值 )
更新OPEN表中的估价值;}
else //Y在CLOSE表中 {
if( Y的估价值小于CLOSE表的估价值 ){
更新CLOSE表中的估价值;
从CLOSE表中移出节点,并放入OPEN表中;}
}
将X节点插入CLOSE表中;
按照估价值将OPEN表中的节点排序;
}//end for
}//end while
}//end function
5 结 语
分析AStar算法原则后,不难发现AStar算法由于采用估价函数,对各个节点进行评估以确定最有可能到达目标的节点,即“最佳节点”,从而极大地减少了对状态空间的搜索过程,使其能快速求解出一条最佳路径。估价函数的合理性直接决定AStar算法的执行效率,合理的估价函数能极大提高算法效率。这使得AStar算法具体应用时,应根据实际需要设计启发值,即确定估价函数,以使求解最优。
如应用于自驾车路线时,节点n到目标的最短路径的启发值h′(n)可由第n点的经纬度和目标点的经纬度通过距离计算得到。
参 考 文 献
[1]蔡自兴.人工智能及其应用[M].北京:清华大学出版社,1997.
[2]NilssonNJ.人工智能[M].郑扣根,庄越挺,译.北京:机械工业出版社,2000.
[3]严蔚敏,吴伟民.数据结构[M] 北京:清华大学出版社,1999.
[4]丛明煜,王丽萍.现代启发式算法理论研究[J].高技术通讯,2003,13(5):105110.
[5]王潇潇,韩家新,马刚.一种启发式的足球机器人传球路径搜索算法\.现代电子技术,2007,30(20):7576,79.
作者简介 张 胜 男,1979年出生,湖北潜江人,讲师。主要研究方向为信息系统集成、数据挖掘。
















