混合遗传算法的带时间窗卷烟物流车辆路径优化
摘 要: 车辆路径问题(VRP)是物流配送的关键环节,优秀的配送策略可帮助企业提高服务体验,降低服务成本。在卷烟物流配送系统中会面临需求点数量巨大,客户指定接受服务的时间段要求。通过研究此类大范围卷烟配送的路径优化问题,结合实际需求,构建卷烟物流路径优化数学模型,并运用遗传算法处理该问题,提出以遗传算法为基础,爬山算法局部寻优的混合遗传算法。通过算例Matlab仿真计算,优化后的混合算法较一般的遗传算法可以提高算法收敛速度,并提升算法的全局最优解的质量。
关键词: 混合遗传算法; 爬山算法; 路径优化; 烟草配送; 物流配送; Matlab
中图分类号: TN911.1?34; TP301.6 文献标识码: A 文章编号: 1004?373X(2018)11?0119?05
Hybrid genetic algorithm based cigarette logistics vehicle routing
optimization with time window
FAN Wenbing, FENG Wen
(School of Information Engineering, Zhengzhou University, Zhengzhou 450001, China)
Abstract: The vehicle routing problem (VRP) is the key link in logistics distribution. The excellent distribution strategy can improve the service experience and reduce the service cost for enterprises. In cigarette logistics distribution system, it is faced with the problems of a huge number of demand points and specified service time required by customer. In this paper, the route optimization problem for wide range cigarette distribution is studied, the actual demand is combined to construct the route optimization mathematical model of cigarette logistics, and the genetic algorithm is used to deal with the problem. On the basis of genetic algorithm, the hybrid genetic algorithm combining mountain climbing algorithm is put forward for local optimization. The example is calculated with Matlab simulation. The simulation results show that, in comparison with the general genetic algorithm, the optimized hybrid genetic algorithm can improve the convergence speed, and promote the quality of the global optimal solution.
Keywords: hybrid genetic algorithm; mountain climbing algorithm; path optimization; tobacco distribution; logistics distribution; Matlab
0 引 言
中国每年烟叶种植面积及烟草制品的产销售量均占到世界总量的[13],其中,卷烟的产量居世界第一。提高我国烟草行业的管理水平,降低烟草经营成本,对国民经济与财政收入的增加都有非常重要的战略意义。在物流企业安排配送行为中,通常会提供多种配送方案以供选择,但每种方案伴随着不同的运输成本,对企业而言,在满足约束条件的前提下,选择经济有效的配送策略就成为降低企业运营成本的重要手段之一。
在卷烟配送物流领域中,物流配送的路径优化实际上是一个NP问题,解决此类问题时,在配送节点较多的情况下通常使用傳统的算法,但求解的结果并不满意。遗传算法是一种有效的全局搜索算法,它具有运算简单、收敛速度快的特点,然而,遗传算法在局域寻优方面能力并不出众。爬山算法是一种局部能力搜索较强的算法,恰好能弥补遗传算法在局部搜索方面的不足。本文尝试将两种算法结合,建立爬山遗传算法模型解决卷烟物流配送的路径优化问题,并结合实例验证和性能分析证明其可行性。
1 卷烟物流配送路径优化数学模型建立
卷烟物流配送行为中一般会有一个配送中心与多个需求客户点,卷烟配送时使用的车辆数、经过的线路、配送路径的合理性、客户需要接受服务的时间窗对配送效率、配送成本有着直接的影响。采用正确的算法确定配送策略,制定优秀合理的车辆路径规划是卷烟物流管理中极其重要的一项工作。优化车辆配送路径具有多种选择,结合卷烟配送的实际情况而定。假设仅有一个配送中心,不限数量、同等规格的配送车辆供使用,向多个有时间要求的需求点送货,每个配送点有坐标和配送量以及接受服务的时间区间。如果配送时间没有在需求点区间内配送,则会产生一定的时间成本,因此,合理高效的配送策略使得配送的总体成本最低,客户满意度最高。确定配送路线策略的优化目标需考虑如下几点:
1) 优化车辆配送策略,使得该方案消耗的成本最低;
2) 按照需求点的要求时间窗送货,以此提高客户体验;
3) 在满足需求点需求的前提条件下,一个需求点有且只能由一辆配送车辆完成。
综上所述,优化的卷烟物流配送路径问题可以表述如下:企业拥有配送车辆[K]辆,每辆车的最大载重量为[Q],现有[n]个客户需求点[1,2,…,n]对卷烟有不同需求,第i个客户需求点的需求量是[dii=1,2,…,n]且有[max di≤Q],即每个点需求一辆车可以完成,车辆到达客户[i]的时间为[si],完成客户[i]的需求需要耗时[Ti],需求点接受服务时间区间为[ei,li],即配送车辆到达客户[i]会早于[ei],则车辆会在[i]处等待并产生等候成本;若迟于[li],则会产生延迟惩罚成本,设定配送车辆单位运输距离的成本为[α],单位车辆的启用固定成本为[β],车辆由客户[i]行驶到客户[j]的时间,且[i≠j],每个客户能且只能由一辆配送车辆一次完成运送任务,每辆车从配送中心出发且最终返回中心。最终目标是在如下约束条件下找出卷烟配送行为发生成本最低的配送策略。根据以上假设得出如下模型:
[min Fi,j,k=αk=1Kj=0Ni=0Ncijxijk+βk=1Kj=1Nx0jk+k=1Kj=1NPisi] (1)
[s.t. k=1Kj=1Nxijk≤K, i=0] (2)
[j=1Nxijk=j=1Nxijk≤1, i=0, k∈1,2,…,K] (3)
[k=1Kj=0Nxijk=1, i∈1,2,…,N] (4)
[k=1Ni=0Nxijk=1, j∈1,2,…,N] (5)
[i=0Nj=0Ndixijk≤Q, k∈1,2,…,K] (6)
[i=0Nxip-j=0Nxpj=0, p∈1,2,…,N, k∈1,2,…,K] (7)
[Tk0+i=0Nj=0Nxijktij+fi+wi≤TkR, k∈1,2,…,K] (8)
[k=1Ki=0Nxijksi+fi+wi+tij=sj, j∈1,2,…,K] (9)
[xijk∈0,1, i,j∈1,2,…,N, k∈1,2,…,K] (10)
[Pi(si)=pmaxei-si,0+qmax(si-li,0)] (11)
[Pi(si)=p(ei-si),0,q(si-li),si
其中:式(1)表示最优化路径的总成本,由车辆行驶距离成本、车辆启用数目成本以及非服务窗服务惩罚成本三项成本构成;式(2)表示可以进行配送行为的运输工具数量上限为[K];式(3)表示每辆车初始点与终点均在配送中心;式(4),式(5)表示每个客户需求点只能被一个配送车辆服务一次;式(6)表示每辆车的载重上限可以满足车上所需完成任务的需求总量;式(7)表示车辆到达服务点,并在完成服务之后离开该服务点;式(8)表示配送行为可以在中心的规定时间内完成;式(9)表示配送车辆从[i]到达需求点[j]的时间约束;式(10)为整数化约束,即限制了[xijk]只能取0或1;式(11)是由式(12)整合得来的惩罚成本表达式。
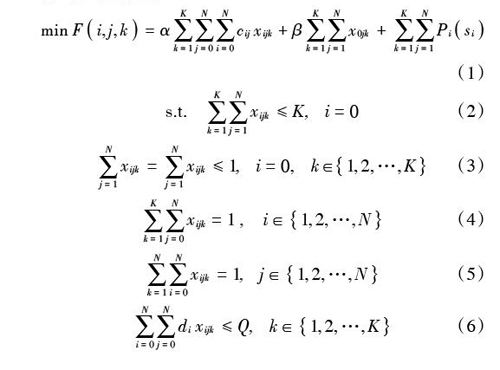
上述模型包含了TSP以及VRP(Vehicle Routing Problem)中一般性的问题。模型考虑的目标函数和约束条件比较全面,接近實际问题,得到的解也为实际问题的全局解,对解决实际问题具有良好的参考意义。
2 相关算法概述
2.1 遗传算法概述
遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,模拟生物在自然环境中优胜劣汰、适者生存的遗传和进化过程,是以适者生存规律进行全局寻优的一种算法,算法使得最具有生存能力的染色体以最大可能生存。最优化问题与生物进化规则的共同点使得最优化问题可以使用遗传算法求得最优解。
2.2 爬山算法概述
爬山算法是一种局部寻优效果好,全局寻优效果较弱的搜索算法。首先在搜索空间随机选取一点作为迭代的初始点;然后在其邻域随机搜索一点,计算其函数值,若该点的函数值优于原始点,则以该点为初始点继续搜索,反之,则继续搜索另一点与初始点进行对比,若连续几次搜索不到更优秀的点则终止搜索过程。
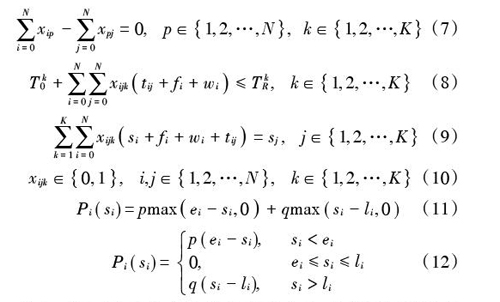
爬山算法在处理局部寻优问题时可以快速收敛到最优解,但是全域寻优问题有多个局部最优点,爬山算法只能找到其中一个局部最优点。尽管爬山算法不能用于全局寻优,但是爬山算法可以通过在邻域内随机搜寻个体进行优化,不需要利用梯度,所以在遗传算法处理复杂问题时,爬山算法可以辅助遗传算法进行局部寻优,以提高收敛性以及算法精度。
为了改进遗传算法,将求局部寻优较好的爬山算法置于遗传算法中,作为一个独立的算子,以避免遗传算法陷入局部解,并提高遗传算法的收敛速度及精度。
3 算法实现操作
3.1 染色体编码
地基对于高楼,相当于编解码方式对于遗传算法,选择合适的编解码方式是算法的根基。根据实际问题的需求不同,专家学者提出不同的编解码策略。可以分为:实数编码、二进制编码、整数或字母排列编码和针对具体问题的数据结构编码等。本研究要解决的卷烟配送路径优化问题是组合优化问题,对染色体采用基于需求点的自然数编码方式。
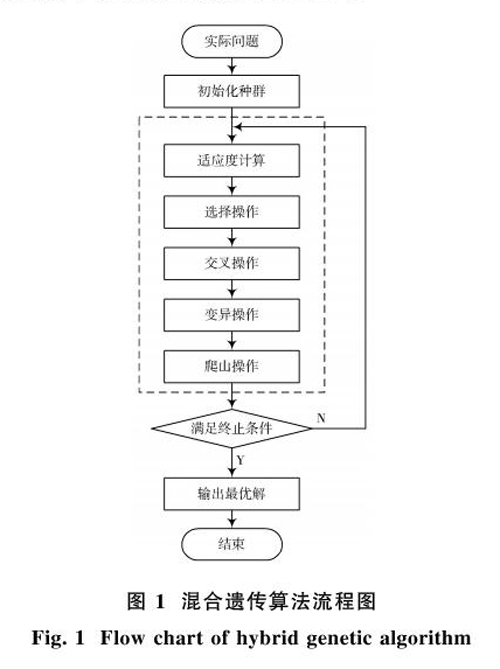
假设用3辆配送车辆对9个需求点进行配送,得到的个体编码为(0 3 2 5 0 7 9 6 4 0 1 8 0),其中,0表示配送中心,则该染色体表示的路径方案为:子路径1:(0?3?2?5?0);子路径2:(0?7?9?6?4);子路径3:(0?1?8?0)。以配送中心0作为不同子路径的分隔符使得每个染色体可以很直观地看清路径分配,由于这种编码方式会给之后的交叉操作带来大量的无用解,为了避免这种情况的发生,本研究采用的编码策略是在染色体中不体现分割位,染色体为全部路径连续排布,对于以上染色体在本文的编码方式为(3 2 5 7 9 6 4 1 8),可大大简化对模型约束条件的处理。
3.2 适应度函数
“适者生存,优胜劣汰”是自然界生物进化过程中的核心自然法则,物种的环境适应能力是衡量该物种质量优劣的基本标准。同样地,适应度是遗传算法中评判个体质量是否优秀的标准。本研究是最小化组合优化问题,目的是配送总成本最小,即目标函数的值最小,通过如下方式将目标函数转化为适应度:
[fi=1zi, i∈1,2,…,popsize] (13)
式中:[zi]种群中第[i]条染色体对应方案的解是第[i]条染色体方案消耗的配送成本;[fi]是第[i]条染色体对应的适应度数值,其值越大,则子代拥有其特性的概率越大。
3.3 交叉算子
在当代自然科学中,生物进化与遗传的实质是两个拥有其各自特性基因的染色体互相融合交叉的过程,遗传算法中引用了颇为重要的交叉算子,用来重现进化过程中的交配重组。一方面,保留了原始群体中优良个体的特性;另一方面,它促使新的个体出现,并保持了新一代种群的个体多样性。本文采用的方法是部分匹配交叉法(Partially Matched Exchange,PMX)。PMX方法与传统的交叉算子有所不同,并不是直接交换原染色体的交叉段,而是先将交叉段放置于原染色体首个基因之前,之后再逐一去掉原染色体中相同的基因。假设共有9个需求点,有两个染色体[A(123456789)],[B(987654321)],之后随机产生两个交叉位,并将交叉位中间的基因互置于两个原染色体首个基因之前,最后将原染色体中相同的基因去除并获得新的染色体个体,例如,选择三号位和七号位为交叉点得到[A123|4567|89],[B987|6543|21],互置操作后得到[A6543|123456789],[B4567|987654321],去掉重复基因后获得新个体[A1654312789],[B1456798321]。相比传统单点交叉和多点交叉等方法,PMX确保即使两个相同个体交叉后依然能获得新个体,从而避免早熟现象,降低了结果为局部最优解的概率。
[A:123456789B:987654321?选取交叉位?A:123|4567|89B:987|6543|21?交叉去互置?A:6543|123456789B:4567|987654321?删除重复基因?A1:654312789B1:456798321]
3.4 变异算子
物种的进化离不开变异现象,这也保证了物种多样性的存留,在算法中引入变异算子来体现物种变异现象,并设定其概率一般为[0~0.02]。物种变异的可能性比较小,因此在遗传算法中变异算子主要是辅助进化的作用,但其在保持种群多样性,避免早熟等方面也有很重要的作用,改善了遗传操作搜索全局解的性能。本文采用随机倒序方式来产生变异,例如:
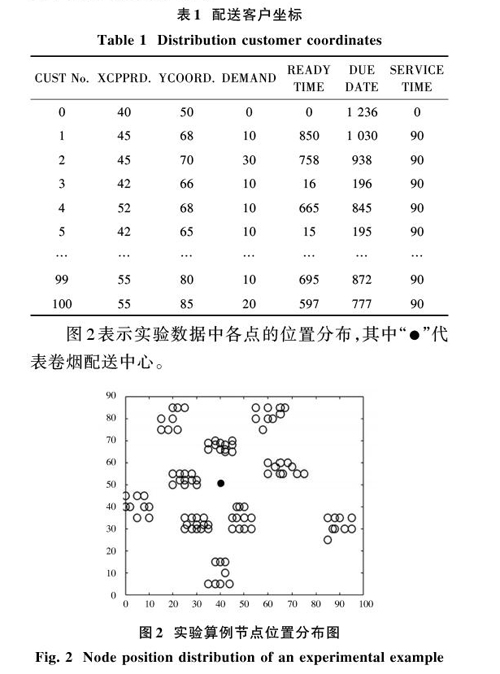
[A123456789?A123|45678|9?A1123876549]
3.5 终止进化规则
遗传算法属于随机搜索算法,在算法进行时必须预先设定终止进化规则以结束遗传算法的演化循环,当算法满足预先设定的终止规则时停止迭代,预先设定进化代数能可靠控制遗传算法的运算时间以及求解精度,因此,本文采用事先确定进化代数作为终止规则,当迭代次数达到预先值时,终止算法循环,并导出最优解;否则,算法将继续循环并将循环次数累加。
3.6 算法步骤
遗传算法的具体步骤如下:
Step1: 使用算例数据,随机产生配送路线的初代种群;
Step2: 设置算法参数和终止条件,如[α,β,p,q,Pc,][Pm,Gen]等;
Setp3: 标记进化代数为0,随机生成[N]个染色体,按照基于排序和最佳个体保存策略的轮盘赌法改进下一代;
Step4: 计算各染色体适应度,使用PMX交叉算子完成交叉步骤,使用变异算子进行随机变异步骤,重组新种群,进行爬山操作,标记迭代次数加1;
Step5: 判断是否达到终止条件,如果达到,则输出配送路径、成本以及迭代代数,否则,跳转到Step4。
4 混合遗传算法中的爬山操作
算法得到的新代种群中都会有最优个体,对其进行爬山操作,可以有效防止遗传算法陷入局部最优解,并且提高算法的收敛性。为了遗传爬山混合算法的实现,本文提出将求局部最优解算法较好的爬山算法置入遗传算法中,作为其中一个独立的步骤,采用基因互换方法进行爬山操作:以新一代种群中的最优个体为对象,对其随机两个基因进行互换操作,若互换后的结果优于原始个体则取代原个体,重复爬山操作到一定的交换次数位为止。其具体算法流程图见图1。
5 仿真验证与性能分析
5.1 实验数据
求解本文问题的运算环境如下:处理器为Intel Core i5?4590,内存为4 GB,操作系统为Windos 10,Matlab运行版本为R2015b。
本文假设有100个需求点需要配送,配送数据包含每个需求点的坐标、需求量、最早接受服务时间、最晚接受服务时间、服务时间等参数,如表1所示。配送中心坐标为(40,50)。具体实验数据请参考Solomon在1983年设计的标准测试题库Benchmark Problems中的C107算例。
表1中第一列为卷烟配送中心和客户需求点编号;第二列、第三列分别代表该点的[x]坐标和[y]坐标;第四列的数值表示客户需求点所需的卷烟量;第五列、第六列是客户需求点接受服务的时间区间;第七列代表服务该需求点需要使用的时间。

图2表示实验数据中各点的位置分布,其中“●”代表卷烟配送中心。
5.2 实验参数设定
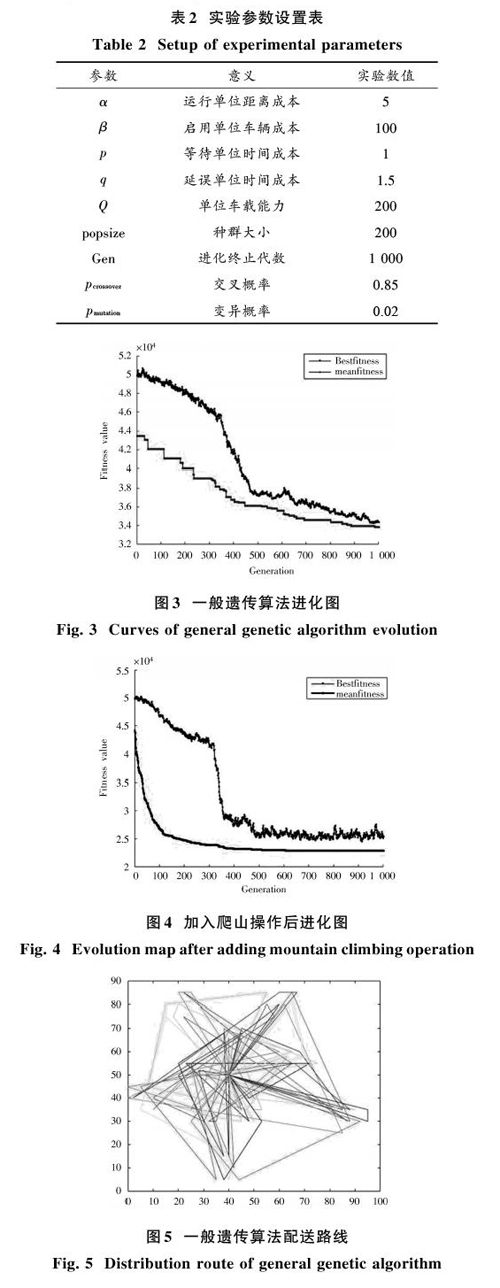
本文使用C107算例作为实验数据,求解本文所需解决的问题。在求解过程中,设定相关实验参数如表2所示。
5.3 混合爬山遗传算法比较
将爬山操作嵌入原始算法之后,依次运用原始方案与新方案对C107算例进行10次求解,得到两种方案的对比结果如图3~图6,表3所示。
6 结 论
本文以遗传算法为蓝本,嵌入爬山操作,全面改善了遗传算法的性能,增强了遗传算法在解决卷烟物流配送路径优化中的收敛速度与计算精度,避免陷入局域解,使遗传算法的功效得到了极大提高。实验结果表明,该算法是求解带时间窗卷烟物流车辆路径优化问题的一个较好方案。
参考文献
[1] 赵丽,陈勇.卷烟物流非劣排序遗传多目标优化配送策略[J].物流技术,2015,34(9):170?173.
ZHAO Li, CHEN Yong. Non inferior sorting genetic multi?objective optimal distribution strategy for cigarette logistics [J]. Logistics technology, 2015, 34(9): 170?173.
[2] 刘家利,马祖军.存在车辆租赁及共享且有时间窗的多配送中心开环VRP[J].系统工程理论与实践,2013,33(3):666?675.
LIU Jiali, MA Zujun. Open loop VRP with multiple distribution centers with vehicle rental and sharing and time windows [J]. Theory and practice of system engineering, 2013, 33(3): 666?675.
[3] 代颖,马祖军.应急物流系统中的随机定位?路径问题[J].系统管理学报,2012,21(2):212?217.
DAI Ying, MA Zujun. Random positioning path problem in emergency logistics system [J]. Journal of system management, 2012, 21(2): 212?217.
[4] 田炳丽,刘常波,解贵新.旋转货架拣选作业优化的交叉蚁群算法求解[J].现代电子技术,2008,31(12):161?164.
TIAN Bingli, LIU Changbo, XIE Guixin. Cross ACO algorithm for optimization of picking operation of rotating shelves [J]. Modern electronics technique, 2008, 31(12): 161?164.
[5] 于蕾,吴强.一个基于社区相似度分析的物流网络优化算法[J].现代电子技术,2016,39(6):45?48.
YU Lei, WU Qiang. A logistics network optimization algorithm based on community similarity analysis [J]. Modern electronics technique, 2016, 39(6): 45?48.
[6] STUDLAR D T. Tobacco control: comparative politics in the United States and Canada [M]. Toronto: University of Toronto Press, 2002.
[7] TEUNTER R. Lot?sizing for inventory systems with product recovery [J]. Computers and industrial engineering, 2012, 120(46): 431?441.
[8] WARK P, HOLT J. A repeated matching heuristic for the vehicle routing problem [J]. Operations research society, 1994, 45(10): 1156?1167.
[9] WANG Xiaowan, LUO Zhengshan, LI Zhou. Research of vehicle dispatch based on GIS logistic distribution and delivery [J]. Statistics and decision, 2011(2): 54?56.
[10] YANG Qing, WEI Zhongbang. A study on logistics distribution system based on ArcGIS engine [J]. Science of surveying and mapping, 2010(35): 149?151.
[11] RAWLS C G, TURNQUIST M A. Pre?positioning of emergency supplies for disaster response [J]. Transportation research part B: methodological, 2010, 44(4): 521?534.
[12] EBADA R, MESBAH S, KOSBA E, et al. A GIS?based DSS for evacuation planning [C]// The 22nd International Conference on Computer Theory and Applications. [S.l.]: IEEE, 2012: 35?40.
















