融合空时符号相干和特征空间波束形成的超声成像
摘 要: 为了进一步提高超声成像的质量,提出融合特征空間最小波束形成和空时符号相干系数的成像方法。首先利用最小方差法计算回波数据的协方差矩阵和加权向量;然后对协方差矩阵进行特征分解得到信号子空间,并将加权向量投影到信号子空间,得到特征空间方法的加权向量,同时采用空时平滑方法计算符号相干系数;最后用空时符号相干系数作为加权系数对特征空间最小方差波束形成的结果进行优化。为了验证算法的有效性,对医学成像上常用的点目标和斑目标进行成像。仿真实验结果表明,与特征空间最小方差算法和融合特征空间与相干系数的算法相比,所提方法提高了对比度和稳健性,其代价是略微降低了成像分辨率。
关键词: 自适应波束形成; 特征分解; 特征空间; 空时符号相干系数; 超声成像; 波束优化
中图分类号: TN911.73?34 文献标识码: A 文章编号: 1004?373X(2018)11?0036?04
Ultrasound imaging algorithm combining eigenspace?based
beamforming and spatio?temporal sign coherence factor
MENG Deming1, 2, 3, LI Xiaodong1, HE Xiaonian2, 3
(1. Guilin University of Electronic Technology, Guilin 541004, China; 2. Health Science Center, Shenzhen University, Shenzhen 518060, China;
3. National?Regional Key Technology Engineering Laboratory for Medical Ultrasound, Shenzhen 518060, China)
Abstract: An imaging method combining eigenspace?based minimum variance (ESBMV) beamforming and spatio?temporal sign coherence factor (STSCF) is proposed to improve the quality of ultrasound imaging. The minimum variance beamforming method is used to calculate the covariance matrix and weight vector of the echo data. The feature decomposition is performed for the covariance matrix to obtain the signal subspace, and then the weight vector is projected into the signal subspace to obtain the weight vector of the eigenspace method. The spatio?temporal smoothing method is used to calculate the sign coherence factor. The spatio?temporal sign coherence factor is deemed as the weighting coefficient to optimize the results of eigenspace?based minimum variance beamforming. The point scatters and cyst phantom commonly used in medical imaging are imaged to verify the validity of the algorithm. The simulation results show that, in comparison with the eigenspace?based minimum variance algorithm and the algorithm combining eigenspace and coherence factor, the proposed algorithm can improve the contrast and robustness, whose shortcoming is to reduce the imaging resolution slightly.
Keywords: adaptive beamforming; feature decomposition; eigenspace; spatio?temporal sign coherence factor; ultrasound imaging; wave beam optimization
0 引 言
医学超声成像中延时叠加(Delay?and?Sum,DAS) 波束形成方法未考虑回波信号特性,导致成像空间分辨率较低,对比度较差[1?2]。自适应最小方差(Minimum Variance,MV)波束形成算法根据回波信号的特征计算各通道加权值,提高了超声成像的质量[3]。由于医学超声信号的高相关性、宽带等特点[4],协方差矩阵计算时会出现奇异矩阵的现象。文献[5]采用空间平滑技术、解相关回波信号,获得更精确的协方差矩阵的估计;文献[6]采用前后向空间平滑法去除回波信号的相关性;文献[7]提出对角加载方法,通过获得稳健的协方差矩阵来提高MV算法的鲁棒性。文献[8]提出特征空间最小方差波束形算法(Eigenspace?based MV,ESBMV),进一步去除噪声和干扰信号对成像结果的影响,获得了高对比度和高分辨率的医学超声图像。
文献[9?10]中提出用相干系数CF(Coherence Factor)評价成像质量方法。文献[11]将相干系数引入到最小方差波束形成算法中,利用相干系数弥补了MV算法对比度不高的缺点,提高了超声成像对比度,文献[12]将相位相干系数PCF(Phase Coherence Factor)引入到最小方差波束形成算法中,提高了成像的分辨率。文献[13]提出一种基于最小方差的相干系数,并应用于平面波成像中,提高了成像对比度。文献[14]将相干系数引入到特征空间最小方差波束形成算法中,进一步提高了超声成像的分辨率。文献[15]提出融合特征空间波束形成和符号相干系数(Sign Coherence Factor,SCF)融合的成像算法,提高了成像的分辨率。
本文提出一种融合特征空间最小方差波束形成与空时符号相干系数的超声成像算法。该算法利用空时平滑方法计算符号相干系数,优化符号相干系数的计算,提高成像对比度并抑制了黑区伪像。为验证本文所提方法的有效性,将本文所提算法分别与DAS,MV,ESBMV,ESBMV_CF,ESBMV_SCF算法进行比较。
1 算 法
1.1 信号模型和最小方差波束形成
一个由[M]个等间距的阵元组成的线性换能器接收了近场内散射目标的反射信号,则波束形成的输出可表示为:
[y(k)=wH(k)xd(k)=i=1Mwi(k)xi(k-Δi)] (1)
式中:[k]表示时间系数;[xd(k)=[x1(k-Δ1),x2(k-Δ2),…,][xM(k-ΔM)]T]为聚焦延时后的信号;[w(k)=[w1(1),][w2(2),…,][wM(M)]T]为加权向量;[Δi]为各通道延时。当[w(k)]为全1向量时,波束形成方法退化为传统DAS算法。
最小方差波束形成算法的基本思想是在期望信号增益不变的情况下,通过使阵列的输出能量最小化的方法,寻找最优的加权向量[w]。其数学表达式为[7]:[minwwHRi+nws.t. wHa=1] (2)
式中:[Ri+n]是干扰加噪声的协方差矩阵;[a]为方向向量,经过延时聚焦后,[a]表示为[a=[1,1,…,1]],由此可得加权矢量为:
[wMV=R-1i+naaHR-1i+na] (3)
在实际应用中,用回波信号的采样协方差矩阵[R]取代式(3)中的协方差矩阵。为了去除回波信号的相关性,利用空间平滑方法重构采样协方差矩阵:
[R=1M-L+1l=1M-L+1xld(k)xld(k)H] (4)
式中[xld(k)=[xld(k),xl+1d(k),…,xl+L-1d(k)]T]为第[l]个子阵的输出向量,则空间平滑后的输出为:
[y(k)=1M-L+1l=1M-L+1wHMV(k)xld(k)] (5)
1.2 特征空间最小方差波束形成
在特征空间波束形成(ESBMV)方法中,将协方差矩阵分解为信号子空间和噪声子空间,然后由MV算法中加权向量[wMV]投影到信号子空间中[3],进一步降低了旁瓣信号幅度。协方差矩阵的特征分解可以表示为:
[R(k)=EsΛsEHs+EnΛnEHn] (6)
设[λi]为特征值,将[R(k)]的特征值由大到小排列:[λ1>][λ2>…>λi…>λL]。[Λs=diag(λ1,λ2,…,λnum)]对应特征向量为[Es],[Λn=diag(λnum,λnum+1,…,λL)]对应特征向量为[En]。[Es]和[En]分别对应信号子空间和噪声子空间,num为信号子空间的维数,num的大小决定了特征值分解方法保持主瓣和压低旁瓣信号的能力,通常用大于最大特征值[α]倍特征向量个数决定,其中[α]的取值范围为0.1~0.5。将[wMV]投影到信号子空间,得到ESBMV的加权向量为:
[wESBMV=EsEHswMV] (7)
由此得到的ESBMV波束形成的最终输出为:
[y(k)=1M-L+1l=1M-L+1wHESBMV(k)xld(k)] (8)
1.3 空时平滑符号相干系数
相干系数反映了回波信号的相干程度,其定义可以表示为:
[CF(k)=m=0M-1xm(k)2Mm=0M-1xm(k)2] (9)
CF用信号幅度分布来表示,PCF用相位分布来表示信号相关程度,SCF是相位相干的特殊情况,用接收信号的正负重构信号,即信号符号位[bi(k)]表示采样点的值[15]。
由于回波信号的随机性,为了降低相干的变化对最终成像的影响,利用空时平滑方法修正相干系数,空时平滑的相干系数表示为[16]:
[STCF(k)=n=-KKl=0M-Lm=l L+l-1xm(k,n)2(M-L+1)n=-KKl=0M-Lm=lL+l-1xm(k,n)2] (10)
式中:[M]为阵列的阵元数;[L]为子阵的长度;[K]为深度方向的采样点数。用[bm(k,n)]替换式(10)中的信号[xm(k,n)],得到一个变量:
[STCFb(k)=n=-KKl=0M-Lm=l L+l-1bm(k,n)2(M-L+1)n=-KKl=0M-Lm=lL+l-1bm(k,n)2] (11)
则空时符号相干系数的表达式为:
[STSCF(k)=1-1-STCFb(k)] (12)
1.4 ESBMV?STSCF算法
特征空间的最小方差波束形成与空时相干系数融合(ESBMV?STSCF)的超声成像算法流程如下:首先采用ESBMV算法对回波信号进行处理,同时计算STSCF系数,最后采用STSCF系数对ESBMV波束形成结果进行加权成像。
对于成像点,根据式(8),式(10),式(12)可得ESBMV?STSCF波束形成的最终输出为:
[y(k)=STSCF(k)1M-L+1l=1M-L+1wHESBMV(k)xld(k)]
2 仿真结果及讨论
为了研究本文所述算法的性能,利用Field Ⅱ进行点射目标和斑散射目标的仿真实验。采用[M=96]阵元线阵换能器,阵元间距为半个波长,设置中心频率[f0=]4 MHz,采样频率[fs=]100 MHz,声速为1 540 m/s,子阵长度[L=][M2]。所有仿真均采用定点聚焦发射和动态接收聚焦的工作模式,仿真成像分别对点散射目标和斑散射目标进行成像。采用DAS算法、MV算法、ESBMV算法、ESBMV?CF算法、ESBMV?SCF和ESBMV?STSCF算法进行成像并对比。对接收回波信号加入60 dB的高斯白噪声。
2.1 点散射目标成像
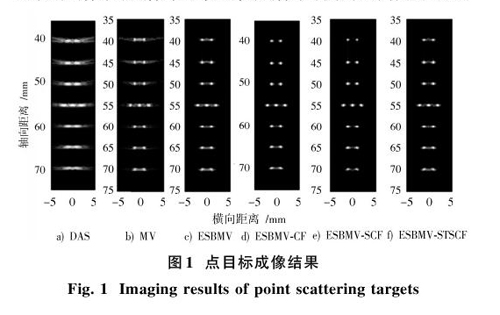
在点散射目标成像时,发射聚焦深度设置为50 mm,成像的动态范围均设定为60 dB。图1为不同方法对不同深度散射点的成像结果,相邻散射点的横向距离为2 mm。
从图1中可以看出,DAS算法的对比度和分辨率最低,MV方法旁瓣等级有所降低,提高了分辨率;ESBMV算法ESBMV?CF主瓣宽度与MV算法相似,旁瓣降低明显;ESBMV?SCF算法进一步降低了旁瓣等级,成像的分辨率和对比度最好。与ESBMV?SCF算法相比,ESBMV?STSCF算法采用空时平滑方法优化了相干系数的计算。但是仅对于点目标的情况下,ESBMV?STSCF算法对旁瓣信号的抑制效果不如ESBMV?SCF算法。
2.2 暗斑散射目标成像
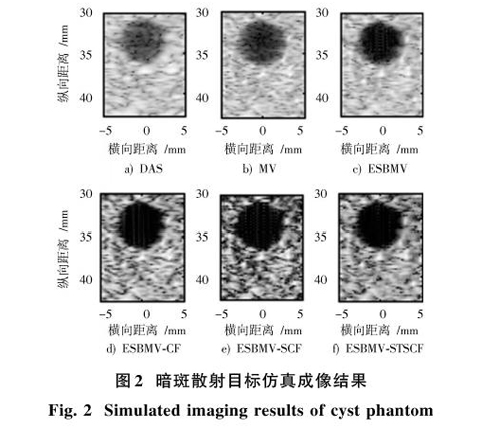
设定组织中有一个圆形暗斑目标,半径均为3 mm,暗斑深度在35 mm处成像的动态范围设定为80 dB。图2为不同算法的成像结果。
從图2可以看出,由于DAS和MV算法的旁瓣抑制能力差,DAS和MV算法的图像对比度很低(见图2a)和图2b));从图2c)可见ESBMV算法能有效抑制旁瓣,提高对比度;ESBMV?CF进一步抑制了旁瓣信号,但由于CF系数的引入,导致图像的整体亮度降低,从而影响了成像质量;当将STSCF引入到ESBMV算法中,利用空时平滑方法得到相干系数更接近真实值,提高了图像对比度和整体成像亮度(见图2f))。
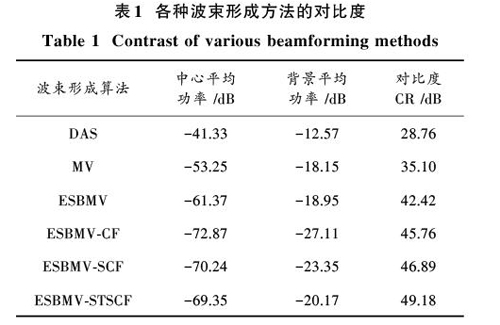
本文引入对比度(CR)[2]来直观评价不同波束形成方法的对比分辨率,其中对比度(CR)定义为中心区域的平均功率与背景区域的平均功率之差。表1列出各种波束形成方法的对比度。
从表1可以看出,ESBMV?STSCF算法的对比度(CR)均优于其他算法。ESBMV类算法中心平均功率明显小于DAS和MV算法,ESBMV?SCF算法中相干系数计算时未考虑到超声回波信号非相干性,抑制了非相干信号,因此ESBMV?SCF算法中心平均功率最小,但背景平均功率下将更显著;ESBMV?STSCF算法优化了相干系数的计算,使得到的相干系数更接近真实值,因此成像对比度优于ESBMV?SCF算法。
3 结 论
本文提出一种特征空间与空时平滑符号相干系数融合的波束形成算法。该算法在保证特征空间法成像分辨率基础上,利用空时平滑方法计算符号相干系数,提升了算法稳定性和成像对比度。通过对点散射目标以及斑散射目标的成像实验,对分辨率、对比度进行比较。结果表明,ESBMV?SCF算法只能针对点散射目标成像获得高分辨率以及高对比度;而对于复杂的斑散射目标成像,本文提出的方法提高了成像对比度。因此,ESBMV?STSCF算法是一种更为有效的波束形成算法。
参考文献
[1] 郑驰超,彭虎.基于编码发射与自适应波束形成的超声成像[J].电子与信息学报,2010,32(4):959?962.
ZHENG Chichao, PENG Hu. Ultrasonic imaging based on coded exciting technology and adaptive beamforming [J]. Journal of electronics and information technology, 2010, 32(4): 959?962.
[2] 王平,许琴,范文政,等.超声成像中基于特征空间的前后向最小方差波束形成[J].声学学报,2013,38(1):65?70.
WANG Ping, XU Qin, FAN Wenzheng, et al. Eigenspace?based for?ward?backward minimum variance beamforming applied to ultrasound imaging [J]. Acta acustica, 2013, 38(1): 65?70.
[3] 吴文焘,蒲杰,吕燚.最小方差波束形成与广义相干系数融合的医学超声成像方法[J].声学学报,2011,36(1):66?72.
WU Wentao, PU Jie, Lü Yi. Medical ultrasound imaging method combining minimum variance beamforming and general coherence factor [J]. Acta acustica, 2011, 36(1): 66?72.
[4] 刘昊霖,易宗锐,刘东权.相干系数与幅度相位估计融合的医学超声成像算法[J].四川大学学报(工程科学版),2015(z2):125?129.
LIU Haolin, YI Zongrui, LIU Dongquan. Amplitude and phase estimation combined coherence factor applied to medical ultrasound imaging [J]. Journal of Sichuan University (engineering science), 2015(S2): 125?129.
[5] SYNNEV?G J F, AUSTENG A, HOLM S. Adaptive beamfor?ming applied to medical ultrasound imaging [J]. IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 2007, 54(8): 1606?1613.
[6] ASL B M, MAHLOOJIFAR A. Contrast enhancement and robustness improvement of adaptive ultrasound imaging using forward?backward minimum variance beamforming [J]. IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 2011, 58(4): 858?867.
[7] LI J, STOICA P, WANG Z. On robust Capon beamforming and diagonal loading [J]. IEEE transactions on signal processing, 2003, 51(7): 1702?1715.
[8] MOHAMMADZADEH A B, MAHLOOJIFAR A. Eigenspace?based minimum variance beamforming applied to medical ultrasound imaging [J]. IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 2010, 57(11): 2381?2390.
[9] HOLLMAN K W, RIGBY K W, O′DONNELL M. Coherence factor of speckle from a multi?row probe [C]// Proceedings of 1999 IEEE Ultrasonics Symposium. [S.l.]: IEEE, 1999: 1257?1260.
[10] MALLART R, FINK M. Adaptive focusing in scattering media through sound?speed inhomogeneities: the Van Cittert Zernike approach and focusing criterion [J]. The Journal of the Acoustical Society of America, 1994, 96(6): 3721?3732.
[11] ASL B M, MAHLOOJIFAR A. Minimum variance beamforming combined with adaptive coherence weighting applied to medical ultrasound imaging [J]. IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 2009, 56(9): 1923?1931.
[12] DING M. Adaptive minimum variance beamforming combined with phase coherence imaging for ultrasound imaging [J]. Proceedings of SPIE: the international society for optical engineering, 2012, 8320: 13.
[13] WANG S L, LI P C. MVDR?based coherence weighting for high?frame?rate adaptive imaging [J]. IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 2009, 56(10): 2097?2110.
[14] ZENG X, CHEN C, WANG Y. Eigenspace?based minimum variance beamformer combined with Wiener postfilter for medical ultrasound imaging [J]. Ultrasonics, 2012, 52(8): 996?1004.
[15] 刘婷婷,周浩,郑音飞.特征空间和符号相干系数融合的最小方差超声波束形成[J].声学学报,2015,40(6):855?862.
LIU Tingting, ZHOU Hao, ZHENG Yinfei. Eigenspace?based minimum variance beamforming combined with sign coherence factor for ultrasound beamforming [J]. Acta acustica, 2015,40(6): 855?862.
[16] XU M, YANG X, DING M, et al. Spatio?temporally smoothed coherence factor for ultrasound imaging [J]. IEEE transactions on ultrasonics ferroelectrics & frequency control, 2014, 61(1): 182?190.
















